Intro to Evolutionary Computation
My last year in college was spent researching Evolutionary Computing. Many people have the wrong idea about how evolution works. When species evolve, they don’t spontaneously and synchronously decide to grow wings or switch from gills to lungs. They are merely adapting to their environment through mutations. Giraffes’ necks weren’t always as long as they are now. There was an evolutionary advantage to the taller creatures who could reach the leaves in trees. These taller creatures had an easier time eating than their shorter relatives and reproduced more as a result. The taller giraffes were the more fit of the population. This is the core principle of survival of the fittest. This is also what we aim to mimic in Evolutionary Computation.
These Three Weird Steps that Created Humans!
In Evolutionary Computation we begin with an input problem that we can score quantitatively. We’ll use the ACT as an example of our input problem. The ACT is a 36-question standardized test for college admission and the goal is to solve the ACT. We begin with a population of 100 children with no knowledge of anything. The children are given a pencil, a test, and a scantron. Initially, they do not know what any of these items are or how they’re used. The test begins and the children have no idea what they are doing. Inevitably, they fail. Each one got a score of 0/36 correct. The first step of Evolutionary Computation has started.
An organism’s fitness is a representation of how well they are doing in their environment. The children got no correct answers, so they each are given a fitness of 0. We now have a choice of how to move forward. We can keep these children or swap them with other children. We swap all of them because they all scored 0.
At this point, the initial 100 children are undergoing selection. During selection, a subset of the population is chosen to survive to the next generation. Selection uses the fitness of each child to determine whether it will survive. At this point the second generation of 100 children are brought in for the test. Once again, they take it and all score 0/36. This process repeats for a while until, by coincidence, a child, Phil, decides to pick up a pencil and scribble on the scantron and sufficiently fill out a C bubble. Phil receives a fitness of 1/36 and the other 99 receive a 0/36. Phil is currently at the peak of evolution. During selection, Phil not only makes it to the next generation, but is cloned. The next population consists of 98 children and 2 copies of Phil. A few more generations go by until the entire population is 100 clones of Phil. There is a problem. Phil will only color in one single C bubble. He will never fill out anything else and will never score more or less than 1/36. We have lost the randomness that was being introduced into our population every generation.
This brings us to the third step, Mutation. We need a way to change Phil’s way of thinking, but only slightly. He got an answer correct so we don’t want to replace him. During mutation, everyone in the population has a small chance to mutate. In the next generation, there are 80 clones of Phil, and 20 mutated Phils. The generation’s scores are as follow:
| Organism | Correct | Possible |
|---|---|---|
| Phil x80 | 1 | 36 |
| Mutated Phil x16 | 1 | 36 |
| Mutated Phil x3 | 0 | 36 |
| Mutated Phil x1 | 2 | 36 |
The originals did not change. 16 of the mutated Phils had no change in behavior. This would mean the mutation was neither harmful or beneficial and is the typical behavior of most mutations. Three of the mutated Phils received a score of 0. This example of a harmful mutation is less usual. Lastly, One mutated Phil, we will call Phip, has received an additional point. A beneficial mutation is typically the rarest. At this point we have a fully functional Genetic Algorithm. Phip will slowly take over the genetic pool until his own mutation, or possibly a mutation from a Phil, yields better results. If we left these children alone for long enough, the cycle of fitness, selection, and mutation would eventually create some ACT prodigy who would score all 36 points.
Genetic Algorithms
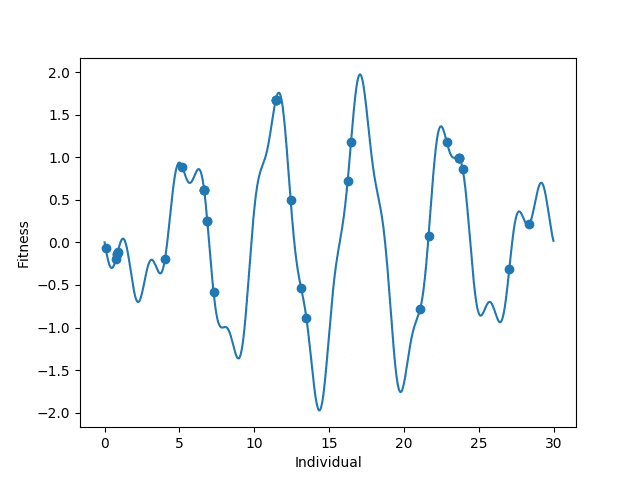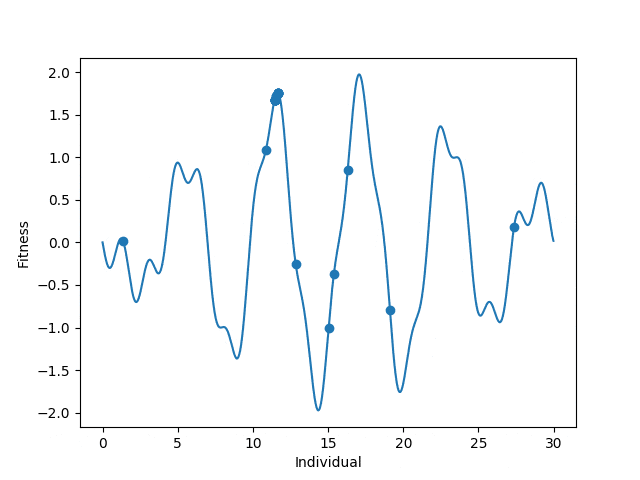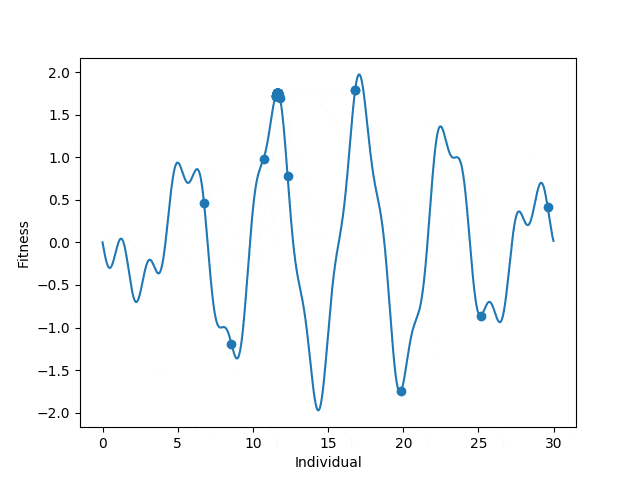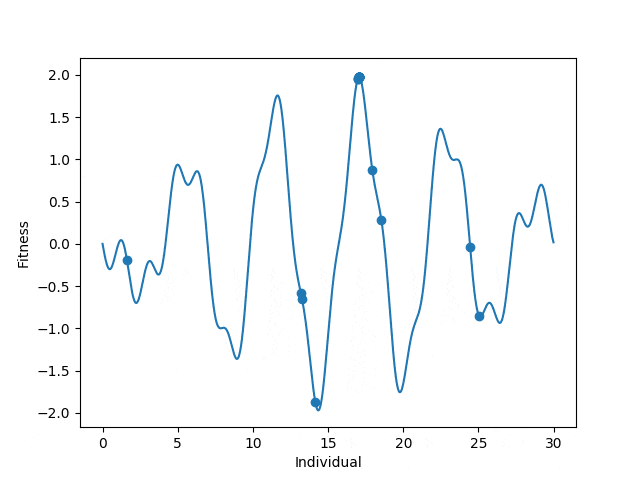
We’ll make a practical example of this in Python by maximizing the function:
y=sin(1.2x)3-sin(x) for 0 ≤ x ≤ 30
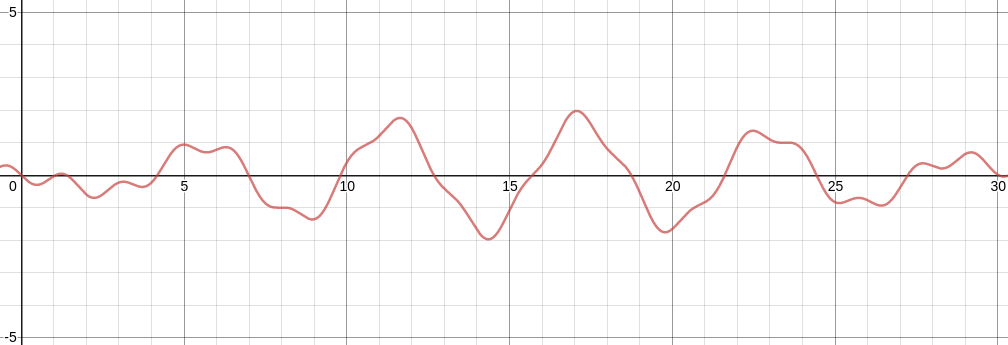
Our first step is to initialize a population.
1
2
3
4
5
from random import uniform
def main():
population = [uniform(0, 30) for _ in range(15)]
The first step will be to create a fitness function. Given an input, our fitness function will tell us how will an individual did. Because we want to maximize our equation, we want a higher y-value. Our fitness function will take in an x-value and return its corresponding y-value.
1
2
3
4
5
from math import sin
def get_fitness(x):
return pow(sin(1.2 * x), 3) - sin(x)
Next we’ll add a selection scheme. There are many different selection schemes with their own use cases. For this I’ll use Tournament Selection. In tournament selection, we randomly select n individuals from the population and let them compete. The winner makes it to the next generation. We repeat this until we have a population for the next generation. In this case, we will have tourney sizes of n=2. We will only fill up 80% of the population pool and fill the rest with random organisms to prevent getting stuck at local maxima.
1
2
3
4
5
6
7
8
9
10
11
12
from random import choice
def get_next_population(population):
next_gen = []
while len(next_gen) < len(population) * 0.8:
a, b = choice(population), choice(population)
winner = max(a, b, key=lambda x: get_fitness(x))
next_gen.append(winner)
while len(next_gen) < len(population):
next_gen.append(uniform(0, 30))
return next_gen
Lastly we’ll create a way for our population to mutate every generation. The mutation operator I’ll choose will be to add a random amount in [-1, 1].
1
2
3
4
5
6
7
8
from random import random
def mutate(population):
MUTATION_CHANCE = 0.2
for i, p in enumerate(population):
if random() < MUTATION_CHANCE:
population[i] = clamp(p + uniform(-1, 1))
To see the full code for the GA, you can visit here.