Learning to Play Flappy Bird through Linear Genetic Programming

Can a flappy bird learn how to fly through obstacles through natural selection and survival of the fittest? This study uses Evolutionary Computation to artificially evolve a program to play Flappy Bird. I previously talked about LinearGP and Evolutionary Computation in my previous post: Artificial Natural Selection

LGPy

In Linear Genetic Programming, a sequence of arm-like instructions represent a program. In developing this project, I began by creating a Python library for Linear GP, inspired by Alex Lalejini’s Signal GP. LGPy is a container that creates virtual hardware. Each hardware contains a program with a set of instructions and a memory buffer of 24 registers by default. Registers hold decimal values clamped between -2³¹ and 2³¹. The catalog of instructions available to a hardware are contained in an instruction library. By default, these include boolean, arithmetic, and comparison operators. Control flow is added to the instruction set as well. PyGP instructions each contain three optional arguments. These arguments can either refer to a literal or a value stored in a register. Instructions can use any subset of these arguments. Take the following two instructions:

1
2

Add 2 4 0
Not 1 3

The Add Instruction takes two source registers and a destination register. It would add the values inside register 2 and 4 and store it in register 0. The Not Instruction takes only one source and one destination register. An instruction pointer will dictate the current instruction to be run at a given CPU cycle. This repeats until it reaches the final instruction, at which point an End of Program flag is set. The instruction pointer can also be modified by the current instruction. Loop-type instructions bind to a following Close instruction to determine the end of the loop. It’s synonymous with a closing curly brace in modern languages. The following is an example of a loop.

1
2
3

While 1
    Sub 1 0 1
Close

Before starting a program, some preprocessing must validate the program. A Close instruction is appended to the end of the program for each unclosed loop-type instruction. If a program is loaded in, each instruction without three arguments is padded with random arguments. The following shows an LGPy example of calculating 10 factorial.

Selection

The selection schemes included in LGPy are Elite, Roulette, Tournament, and Epsilon Lexicase. These selection schemes serve to decide which and how many programs survive to the next generation, potentially generating new programs in the process

Mutations

There are four main mutation operators in LGPy by default. With these, each instruction and argument has a chance to mutate. The Insertion operator adds a random instruction from the instruction library with random arguments to the program. The Delete operator removes an instruction from the program. The Swap operator changes an instruction with another random instruction, but keeps the arguments. Lastly, the Argument Swap operator randomizes an argument in an instruction. By inserting or deleting Close or loop-type instructions, large portions of a program can be changed, making large jumps in the genetic landscape.

Evolving Flappy Bird

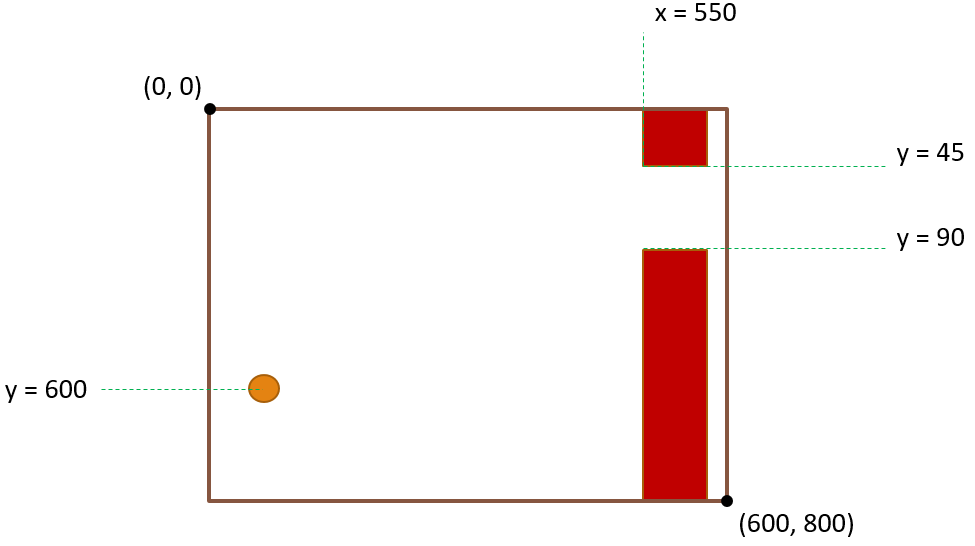
If you’ve never played Flappy Bird before, the objective of the game is to jump through oncoming pipes without crashing into them. A bird locked on the x-axis can either jump up or let gravity bring it down. Each bird is represented asa 32x32 px square. Pipes are represented by two rectangles 100px wide spanning the height of the screen. A gap 256px in height is added to the rectangle randomly for the birds to jump through. If a bird collides with any of the rectangles or the top/bottom of the screen, it will lose. To begin, a population of programs will be initiated with a set of random instructions. Each bird may run a predetermined amount of instructions then pauses and lets the game run a single frame. The default instruction set isn’t enough for the bird to play the game. It must be able to interact with its environment. The following instructions are added the the instruction library:

• GetGapTop - Gets the y-value of the top of the next gap
• GetGapBottom - Gets the y-value of the bottom of the next gap
• GetBirdHeight - Gets the y-value of the center of the bird
• GetScreenHeight - Gets the y value of the top of the screen
• Jump - Sets the birds y-velocity to -10.0 Each frame, a bird’s velocity increases by +0.981. When the Jump instruction is run, the velocity is reset to -10.0.

Scoring

In Flappy Bird, you are given one point for each pipe you cross. However, that is too steep of a learning curve for our programs to evolve. We instead use the following equation to determine score.

A flat bonus f is given to each bird representing the number of frames that have elapsed from the start to the time of the bird crashing. During each frame, the genome is rewarded or punished based on how close the bird’s y-coordinate is to the midpoint of the gap’s y-coordinate. d_i, the absolute distance from the height of the bird and the height of the next closest gap’s midpoint is normalized by g, half the height of a gap and regulated down by a factor of 10. A single, large reward of 50 is given once when a bird’s y-coordinate crosses the y-coordinate of the midpoint. The number of unique gaps’ midpoints a bird crosses in a generation is denoted by x.

Results

Programs are able to evolve that can run indefinitely without running into obstacles. It is worth nothing that the only selection scheme that would evolve a solution is epsilon lexicase. Elite, roulette and tournament all came up with naive solutions that got stuck at local maxima.